ΓΓΓΓ≥θΕΰ «“Μ²ÄÉ…‰OΖ÷Μ·Φ”³ΓΒΡΡξΦâ�����Θ§≥…ΩÉΗζ≤Μ…œΒΡΆ§¨WΆυΆυΈΖë÷îΒ(sh®¥)¨W�Θ§»ί“Ή¹G ßΉ‘–≈–Ρ����Θ§≥…ΩÉά^άm(x®¥)œ¬Μ§ΓΘ≥θ“Μ¦]¨WΚΟ��Θ§ΏÄΩ…Ηζ…œ»ΞΫ¦(j®©ng)Ώ^“ΜΡξΒΡ≥θ÷–¨WΝï�Θ§”–ΒΡΆ§¨WΡήΚήΩλΏmëΣ≥θ÷–ΫΧ¨WΘ§Ά®Ώ^≈§ΝΠ�����Θ§ΏM≤ΫΚή¥σ�����ΘΜ”–ΒΡΆ§¨W≤Μ¥σΏmëΣΘ§Ή‘–≈–Ρœ¬ΫΒ����Θ§≈cΤδΥϊΆ§¨Wά≠¥σΝΥ≤νΨύΓΘ
ΓΓΓΓΚήΕύΜυΒA≤νΒΡΆ§¨WÜ•Έ“��Θ§Έ“èΡ–ΓîΒ(sh®¥)¨WΨΆ≤ΜΚΟ����Θ§§F(xi®Λn)‘Ύ≥θΕΰ≥…ΩÉΏÄ «“ΜΥζΚΐΆΩΘ§Έ“ΏÄ”–Ψ»Üα�ΘΩ‘Ύ¨WΝï≥θΕΰîΒ(sh®¥)¨WΒΡΆ§ïrΘ§Α―“‘«ΑΒΡ÷ΣΉRΚΟΚΟ―a“Μ―a�����Θ§≥…ΩÉ“Μ‰”Ω…“‘Ύs…œ»Ξ����ΓΘ¨Λ’“Ζ÷Μ·‘≠“ρΘ§≤ΜΩ…¹yΆΕαt(y®©) ¬¨ç…œ����Θ§îΒ(sh®¥)¨W≥…ΩÉ“Ζ÷Μ·””–“Μ²ÄùuΏMΒΡΏ^≥Χ�����Θ§ΟΩ²Ä¨WΕΈΕΦ”–≤ΜΆ§ΒΡΖ÷Μ·ϋc��Θ§÷Μ «‘Ύ≥θΕΰΧΊ³eΟςο@��ΓΘ±»»γΒΫ≥θ“Μœ¬¨WΤΎ“―Ϋ¦(j®©ng)”–ΝΥΤΫΟφéΉΚΈ(œύΫΜΨÄ≈cΤΫ––ΨÄ�ΓΔ»ΐΫ«–ΈÉ…’¬)��ΓΔΫβΈωéΉΚΈ(ΤΫΟφ÷±Ϋ«Ήχ‰ΥœΒΒΡ≥θ≤Ϋ÷ΣΉR)ΒΡÉ»»ί�����Θ§¨Π”Ύ≤ΩΖ÷Ώâί΄ΥΦΨSΡήΝΠΚΆΩ’ιgœκœσΡήΝΠί^»θΒΡΆ§¨W�����Θ§¨WΝïΏ@≤ΩΖ÷ΨΆïΰΗ–ΒΫ≥‘ΝΠ�Θ§ΒΪ¥ΥïrΒΡ≥…ΩÉΩ…Ρή≤Μïΰ”–Οςο@ΒΡΆΥ≤Ϋ����Θ§“ρûιΖeάέΒΡÜ•ν}ΏÄ≤ΜΥψΕύΓΘ
ΓΓΓΓ¥σΦ“÷ΣΒά≥θΕΰΒΡ÷Ί“Σ–‘ΝΥÜαΘΩΫώΧλ�Θ§Ϋo¥σΦ“?gu®©)ß¹μ≥θΕΰΒΡéΉΚΈ÷ΣΉRΘ§œΘΆϊΆ§¨W²ÉΡήΚΟΚΟΩ¥Ω¥�����Θ§≥θ»ΐΒΡΆ§¨W“≤Ω…“‘”–ïrιgèΆΝï“Μœ¬����ΘΓ
ΓΓΓΓéΉΚΈΩ…“‘’f’ΦΝΥ≥θ÷–îΒ(sh®¥)¨WΒΡΑκ±ΎΫ≠…ΫΘ§Ρ“ά®ΝΥüoîΒ(sh®¥)ΒΡ÷Ίϋc÷ΣΉR�ΓΔκyϋc÷ΣΉRΓΔüoîΒ(sh®¥)ΒΡ÷–ΩΦΩΦϋc……éΉΚΈ÷ΣΉR÷ς“ΣΦ·÷–‘Ύ≥θΕΰ¨WΝï�����Θ§»γΙϊ≥θΕΰ≤Μ¨WΚΟéΉΚΈ�����Θ§¨ΔïΰΆœάέ’ϊ²Ä≥θ»ΐΘ��Γ�ΘΓ
ΓΓΓΓ‘ΎéΉΚΈÜ•ν}÷–Θ§ΧμΦ”ίo÷ζΨÄΩ…“‘’f «Ϋβν}ΒΡξPφI�ΘΓίo÷ζΨÄ°΄ΒΟΚΟ�Θ§Ϋβν}ίpΥ…”–ΩλΥΌ�ΘΓίo÷ζΨÄ°΄≤Μ¨ΠΘ§Ω…ΡήΨΆ «Ϋβν}ά@èù”÷≥ωεe��ΘΓ»γΚΈΩλΥΌ����ΓΔΧμΦ”άϊ”ΎΫβν}ΒΡίo÷ζΨÄΘΩ��ΘΩ‘EΗ[ΕΦ‘Ύœ¬ΟφΝΥ��ΘΓ
ΓΓΓΓéΉΚΈ≥Θ“äίo÷ζΨÄΩΎ‘E
ΓΓΓΓ»ΐΫ«–Έ
ΓΓΓΓàD÷–”–Ϋ«ΤΫΖ÷ΨÄ�����Θ§Ω…œρÉ…ΏÖΉς¥ΙΨÄ�ΓΘ
ΓΓΓΓ“≤Ω…¨ΔàD¨Π’έΩ¥����Θ§¨ΠΖQ“‘ΚσξPœΒ§F(xi®Λn)ΓΘ
ΓΓΓΓΫ«ΤΫΖ÷ΨÄΤΫ––ΨÄ�Θ§Β»―ϋ»ΐΫ«–Έ¹μΧμΓΘ
ΓΓΓΓΫ«ΤΫΖ÷ΨÄΦ”¥ΙΨÄ�����Θ§»ΐΨÄΚœ“Μ‘΅‘΅Ω¥ΓΘ
ΓΓΓΓΨÄΕΈ¥Ι÷±ΤΫΖ÷ΨÄ����Θ§≥ΘœρÉ…ΕΥΑ―ΨÄΏBΓΘ
ΓΓΓΓΨÄΕΈΚΆ≤νΦΑ±ΕΑκ����Θ§―”ιLΩsΕΧΩ…‘΅ρû����ΓΘ
ΓΓΓΓΨÄΕΈΚΆ≤ν≤ΜΒ» Ϋ�Θ§“ΤΒΫΆ§“Μ»ΐΫ«»Ξ�ΓΘ
ΓΓΓΓ»ΐΫ«–Έ÷–É…÷–ϋcΘ§ΏBΫ”³t≥…÷–ΈΜΨÄ�����ΓΘ
ΓΓΓΓ»ΐΫ«–Έ÷–”–÷–ΨÄ��Θ§±ΕιL÷–ΨÄΒΟ»ΪΒ»��ΓΘ
ΓΓΓΓΥΡΏÖ–Έ
ΓΓΓΓΤΫ––ΥΡΏÖ–Έ≥ω§F(xi®Λn)Θ§¨ΠΖQ÷––ΡΒ»Ζ÷ϋc�ΓΘ
ΓΓΓΓΧί–ΈÜ•ν}«…όD™QΘ§ΉÉ?y®≠u)ι»ΐΫ«ΜρΤΫΥΡΓ?/div>
ΓΓΓΓΤΫ“Τ―ϋ�����Θ§“Τ¨ΠΫ«�Θ§É…―ϋ―”ιLΉς≥ωΗΏΓΘ
ΓΓΓΓ»γΙϊ≥ω§F(xi®Λn)―ϋ÷–ϋcΘ§Φö–ΡΏB…œ÷–ΈΜΨÄ�ΓΘ
ΓΓΓΓ…œ ωΖΫΖ®≤ΜΉύ–ß�����Θ§Ώ^―ϋ÷–ϋc»ΪΒ»‘λ�����ΓΘ
ΓΓΓΓΉCœύΥΤ�����Θ§±»ΨÄΕΈ�����Θ§ΧμΨÄΤΫ––≥…ΝïëT��ΓΘ
ΓΓΓΓΒ»Ζe ΫΉ”±»άΐ™Q��Θ§¨Λ’“ΨÄΕΈΚήξPφI��ΓΘ
ΓΓΓΓ÷±Ϋ”ΉCΟς”–άßκy��Θ§Β»ΝΩ¥ζ™Q…Ό¬ιü©�����ΓΘ
ΓΓΓΓ–±ΏÖ…œΟφΉςΗΏΨÄ�����Θ§±»άΐ÷–콓̥σΤ§����ΓΘ
ΓΓΓΓàA
ΓΓΓΓΑκèΫ≈cœ“ιL”΄ΥψΘ§œ“–ΡΨύ¹μ÷–ιg’Ψ����ΓΘ
ΓΓΓΓàA…œ»τ”–“Μ«–ΨÄΘ§«–ϋcàA–ΡΑκèΫ¬™(li®Δn)�����ΓΘ
ΓΓΓΓ«–ΨÄιLΕ»ΒΡ”΄Υψ��Θ§Ι¥Ι…Ε®άμΉνΖΫ±ψ��ΓΘ
ΓΓΓΓ“ΣœκΉCΟς ««–ΨÄ����Θ§ΑκèΫ¥ΙΨÄΉ–Φö±φΓΘ
ΓΓΓΓ «÷±èΫΘ§≥…ΑκàA��Θ§œκ≥…÷±Ϋ«èΫΏBœ“�����ΓΘ
ΓΓΓΓΜΓ”–÷–ϋcàA–ΡΏB����Θ§¥ΙèΫΕ®άμ“Σ”¦»Ϊ��ΓΘ
ΓΓΓΓàA÷ήΫ«ΏÖÉ…½lœ“�Θ§÷±èΫΚΆœ“ΕΥϋcΏBΓΘ
ΓΓΓΓœ“«–Ϋ«ΏÖ«–ΨÄœ“��Θ§Ά§ΜΓ¨ΠΫ«Β»’“Άξ�ΓΘ
ΓΓΓΓ“ΣœκΉς²ÄΆβΫ”àAΘ§ΗςΏÖΉς≥ω÷–¥ΙΨÄ��ΓΘ
ΓΓΓΓΏÄ“ΣΉς²ÄÉ»Ϋ”àA����Θ§É»Ϋ«ΤΫΖ÷ΨÄâτàAΓΘ
ΓΓΓΓ»γΙϊ”ωΒΫœύΫΜàA�Θ§≤Μ“ΣΆϋΉςΙΪΙ≤œ“ΓΘ
ΓΓΓΓÉ»Άβœύ«–ΒΡÉ…àA����Θ§Ϋ¦(j®©ng)Ώ^«–ϋcΙΪ«–ΨÄ��ΓΘ
ΓΓΓΓ»τ «Χμ…œΏB–ΡΨÄ��Θ§«–ϋcΩœΕ®‘Ύ…œΟφ�����ΓΘ
ΓΓΓΓ“ΣΉςΒ»Ϋ«Χμ²ÄàA��Θ§ΉCΟςν}ΡΩ…Όάßκy����ΓΘ
ΓΓΓΓ”…Ϋ«ΤΫΖ÷ΨÄœκΒΫΒΡίo÷ζΨÄ
ΓΓΓΓ“Μ��ΓΔΫΊ»Γ‰΄»ΪΒ»
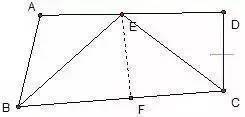
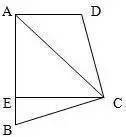
ΓΓΓΓ»γàD����Θ§AB//CD�Θ§BEΤΫΖ÷∠ABCΘ§CEΤΫΖ÷∠BCD��Θ§ϋcE‘ΎAD…œ����Θ§«σΉCΘΚBC=AB+CD����ΓΘ
ΓΓΓΓΖ÷ΈωΘΚ‘Ύ¥Υν}÷–Ω…‘ΎιLΨÄΕΈBC…œΫΊ»ΓBF=ABΘ§‘ΌΉCΟςCF=CD�����Θ§èΡΕχΏ_ΒΫΉCΟςΒΡΡΩΒΡ����ΓΘΏ@άοΟφ”ΟΒΫΝΥΫ«ΤΫΖ÷ΨÄ¹μ‰΄‘λ»ΪΒ»»ΐΫ«–ΈΓΘΝμΆβ“Μ²Ä»ΪΒ»Ή‘“―ΉCΟς�����ΓΘ¥Υν}ΒΡΉCΟς“≤Ω…“‘―”ιLBE≈cCDΒΡ―”ιLΨÄΫΜ”Ύ“Μϋc¹μΉCΟς��ΓΘΉ‘“―‘΅“Μ‘΅�ΓΘ
ΓΓΓΓΕΰΓΔΫ«Ζ÷ΨÄ…œϋcœρÉ…ΏÖΉς¥ΙΨĉ΄»ΪΒ»
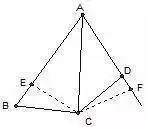
ΓΓΓΓ»γàDΘ§“―÷ΣAB>AD, ∠BAC=∠FAC,CD=BC��ΓΘ«σΉCΘΚ∠ADC+∠B=180
ΓΓΓΓΖ÷ΈωΘΚΩ…”…Cœρ∠BADΒΡÉ…ΏÖΉς¥ΙΨÄ�����ΓΘΫϋΕχΉC∠ADC≈c∠B÷°ΚΆûιΤΫΫ«�ΓΘ
ΓΓΓΓ»ΐΓΔ»ΐΨÄΚœ“Μ‰΄‘λΒ»―ϋ»ΐΫ«–Έ
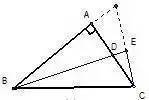
ΓΓΓΓ»γàD��Θ§AB=AC����Θ§∠BAC=90 Θ§ADûι∠ABCΒΡΤΫΖ÷ΨÄ��Θ§CE⊥BE.«σΉCΘΚBD=2CE��ΓΘ
ΓΓΓΓΖ÷ΈωΘΚ―”ιL¥Υ¥ΙΨÄ≈cΝμΆβ“ΜΏÖœύΫΜ��Θ§ΒΟΒΫΒ»―ϋ»ΐΫ«–Έ����Θ§κSΚσ»ΪΒ»ΓΘ
ΓΓΓΓΥΡ��ΓΔΫ«ΤΫΖ÷ΨÄ+ΤΫ––ΨÄ
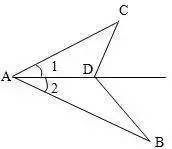
ΓΓΓΓ»γàDΘ§AB>AC, ∠1=∠2�����Θ§«σΉCΘΚABΘ≠AC>BDΘ≠CD�����ΓΘ
ΓΓΓΓΖ÷ΈωΘΚAB…œ»ΓE ΙAC=AE�����Θ§Ά®Ώ^»ΪΒ»ΚΆΫM≥…»ΐΫ«–ΈΏÖΏÖΏÖΒΡξPœΒΩ…ΉC����ΓΘ
ΓΓΓΓ”…ΨÄΕΈΚΆ≤νœκΒΫΒΡίo÷ζΨÄ
ΓΓΓΓΫΊιL―aΕΧΖ®
ΓΓΓΓACΤΫΖ÷∠BAD��Θ§CE⊥AB�Θ§«“∠B+∠D=180°Θ§«σΉCΘΚAE=AD+BE��ΓΘ
ΓΓΓΓΖ÷ΈωΘΚΏ^CϋcΉςAD¥ΙΨÄ��Θ§ΒΟΒΫ»ΪΒ»Φ¥Ω…����ΓΘ
–¬≥θ»ΐΩλ£Ώ¥aξPΉΔ
÷–ΩΦΨW(w®Θng)ΈΔ–≈ΙΪ±äΧ•
ΟΩ»’ΆΤΥΆ¨WΝïΦΦ«…��Θ§¨WΩΤ÷ΣΉRϋc
÷ζΡψ”≠Ϋ”2020Ρξ÷–ΩΦ�ΘΓ
ΓΓΓΓ ög”≠ Ι”Ο ÷ôC��ΓΔΤΫΑεΒ»“Τ³”‘O²δ‘LÜ•÷–ΩΦΨW(w®Θng)�����Θ§2023÷–ΩΦ“Μ¬Ζ≈ψΑιΆ§––��ΘΓ>>ϋc™τ≤ιΩ¥