άϊ”ΟΕΰ¥ΈΚ·îΒ(sh®¥)àDœώ≈–îύΗςœΒîΒ(sh®¥)÷°ιgΒΡξP(gu®Γn)œΒΘ§ «÷–ΩΦîΒ(sh®¥)¨W(xu®Π)ΒΡ≥�ΘΩΦν}–ΆΘ§“ρ?y®Λn)ιΨCΚœ–‘ί^ΗΏΘ§ν}ΡΩί^κy�Θ§Ά®≥ΘΖ≈‘ΎΏx™ών}Μρ’ΏΧνΩ’ν}ΉνΚσ“Μν}Θ§Ήςûι–Γν}ΒΡâΚίSν}�ΓΘ“ρ¥ΥΘ§–η“ΣΗςΈΜΆ§¨W(xu®Π)’J(r®®n)’φ λœΛ¥ΥΖNν}–ΆΒΡΫβν}ΖΫΖ®ΚΆΦΦ«…�ΓΘ
îΒ(sh®¥)¨W(xu®Π)¨W(xu®Π)Νï(x®Σ)
“ΜΓΔΜυ±Ψ‘≠άμΘΚ£¹ΈοΨÄ≈cœΒîΒ(sh®¥)÷°ιgΒΡξP(gu®Γn)œΒ
“―÷ΣΕΰ¥ΈΚ·îΒ(sh®¥)y=ax2+bx+c����Θ§(a≠0, aΓΔb����ΓΔcûιΗςμ½(xi®Λng)œΒîΒ(sh®¥))
1ΓΔa≈c£¹ΈοΨÄΒΡι_ΩΎΖΫœρΦΑ¥σ–Γ÷°ιgΒΡξP(gu®Γn)œΒ
£¹ΈοΨÄι_ΩΎœρ…œ a>0�Θ§
£¹ΈοΨÄι_ΩΎœρœ¬ a<0Θ§
|a|‘Ϋ¥σ�����Θ§£¹ΈοΨÄΒΡι_ΩΎ‘Ϋ–Γ
|a|‘Ϋ–ΓΘ§£¹ΈοΨÄΒΡι_ΩΎ‘Ϋ¥σ
2����ΓΔaΓΔb¦QΕ®£¹ΈοΨÄΒΡ¨Π(du®§)ΖQίS “‘ΦΑ Εΰ¥ΈΚ·îΒ(sh®¥)ΒΡΉν¥σΉν–Γ÷Β
1)£¹ΈοΨĨΠ(du®§)ΖQίSΒΡ±μΏ_(d®Δ) ΫΘΚx= - b/2a
ΔΌ b=0ïr(sh®Σ)�Θ§¨Π(du®§)ΖQίSûιx=0Θ§Φ¥yίS;
ΔΎ°î(d®Γng)a����ΓΔbΆ§Χ•(h®Λo)ïr(sh®Σ)Θ§¨Π(du®§)ΖQίS<0����Θ§Φ¥¨Π(du®§)ΖQίS‘ΎyίSΉσ²»(c®®);
Δέ°î(d®Γng)aΓΔb°êΧ•(h®Λo)ïr(sh®Σ)�����Θ§¨Π(du®§)ΖQίS>0����Θ§Φ¥¨Π(du®§)ΖQίS‘ΎyίS”“²»(c®®);
2)Εΰ¥ΈΚ·îΒ(sh®¥)ΒΡΉν÷Β
ΔΌ °î(d®Γng)a>0ïr(sh®Σ)�Θ§Εΰ¥ΈΚ·îΒ(sh®¥)‘Ύx= - b/2aΧéΘ§»ΓΉν–Γ÷Β(4ac - b²)/4a
ΔΎ °î(d®Γng)a<0ïr(sh®Σ)����Θ§Εΰ¥ΈΚ·îΒ(sh®¥)‘Ύx= - b/2aΧé�Θ§»ΓΉν¥σ÷Β(4ac - b²)/4a
3����ΓΔcΦ¥£¹ΈοΨÄ≈cyίSΒΡΫΜϋc(di®Θn)
“ρ?y®Λn)ι¨?du®§)”ΎΕΰ¥ΈΚ·îΒ(sh®¥)y=ax2+bx+cΘ§°î(d®Γng)x=0ïr(sh®Σ)�����Θ§y=c;
C>0 �ΓΔC=0ΓΔC<0 ����Θ§£¹ΈοΨÄ≈cΉχ‰Υ(bi®Γo)ίSΖ÷³eΫΜ”ΎyίS’ΐΑκίSΓΔ‘≠ϋc(di®Θn)�����ΓΔyίSΊ™(f®¥)ΑκίS�ΓΘ
4ΓΔΓς = b²- 4ac ¦QΕ®£¹ΈοΨÄ≈cxίSΒΡΫΜϋc(di®Θn)²Ä(g®®)îΒ(sh®¥)
ΔΌ °î(d®Γng)Γς > 0ïr(sh®Σ)�����Θ§£¹ΈοΨÄ≈cxίS”–É…²Ä(g®®)ΫΜϋc(di®Θn)
ΔΎ °î(d®Γng)Γς = 0ïr(sh®Σ)Θ§£¹ΈοΨÄ≈cxίS”–“Μ²Ä(g®®)ΫΜϋc(di®Θn)
Δέ °î(d®Γng)Γς <0ïr(sh®Σ)�����Θ§£¹ΈοΨÄ≈cxίSüoΫΜϋc(di®Θn)
Εΰ�ΓΔîΒ(sh®¥)–ΈΫY(ji®Π)ΚœΘΚ¥ζ»κΧΊ β÷Β
‘Ύ¥_Ε®ΝΥ£¹ΈοΨÄΒΡι_ΩΎΖΫœρΓΔ¨Π(du®§)ΖQίS�����ΓΔΉν÷Β�����Θ§“‘ΦΑ≈cΉχ‰Υ(bi®Γo)ίSΒΡΫΜϋc(di®Θn)Κσ�����Θ§ΆυΆυ÷ΜΡήΫβ¦Q«ΑΟφ“Μ–©ί^ûιΚÜ(ji®Θn)ÜΈΒΡÜ•ν}�����ΓΘΈ“²ÉΏÄ–η“Σ“ά™ΰ(j®¥)àD–Έ�����Θ§¥ζ»κΧΊ β÷Β����Θ§≤≈ΡήΫβ¦Qν}ΡΩ÷–ί^κyΒΡÜ•ν}ΓΘ
¥ζ»κΒΡΧΊ β÷Β“ΜΑψ”–x= -1�Θ§ x= 1Θ§ x= -2 ����Θ§x=2Θ§x=¨Π(du®§)ΖQίS Β»�����Θ§“‘ΦΑàD–Έ÷–‰Υ(bi®Γo)≥ωΒΡΧΊ βîΒ(sh®¥)÷Β�����Θ§¨ΔΏ@–©ΧΊ β÷Β¥ζ»κΕΰ¥ΈΚ·îΒ(sh®¥)ΫβΈω Ϋ÷–����Θ§«σ≥ωΚ·îΒ(sh®¥)÷ΒΘ§»ΜΚσΫY(ji®Π)ΚœàDœώ
(1)≈c0Ής±»ί^;
(2)≈cΚ·îΒ(sh®¥)Ήν÷ΒΉς±»ί^;
(3)»γΙϊ”–“Μ¥ΈΚ·îΒ(sh®¥)�����Θ§≈c“Μ¥ΈΚ·îΒ(sh®¥)÷ΒΉς±»ί^;
(4)Μρ’Ώ¥ζ»κΧΊ β÷ΒΚσΘ§¨ΔΒΟΒΫΒΡξP(gu®Γn)”Ύa�ΓΔbΓΔc±μΏ_(d®Δ) ΫΏM(j®§n)––Φ”€p≥Υ≥ΐΏ\(y®¥n)ΥψΒ»����ΓΘ
œ¬ΟφΈ“²ÉΫY(ji®Π)Κœάΐν}ΏM(j®§n)––‘îΦö(x®§)÷vΫβΘΚ
»ΐΓΔάΐν}ΫβΈω
άΐ1����ΓΔ»γàDΥυ ΨΘ§“―÷ΣΕΰ¥ΈΚ·îΒ(sh®¥)y=ax2+bx+cΒΡàDœσ≈cxίSΫΜ”ΎA�����ΓΔBÉ…ϋc(di®Θn)�����Θ§≈cyίSΫΜ”Ύϋc(di®Θn)C����Θ§¨Π(du®§)ΖQίSûι÷±ΨÄx=1.÷±ΨÄy=©¹x+c≈c£¹ΈοΨÄy=ax2+bx+cΫΜ”ΎCΓΔDÉ…ϋc(di®Θn)�����Θ§Dϋc(di®Θn)‘ΎxίSœ¬ΖΫ«“ôMΉχ‰Υ(bi®Γo)–Γ”Ύ3Θ§³tœ¬Ν–ΫY(ji®Π)’™ΘΚΔΌ2a+b+c>0; ΔΎa©¹b+c<0; Δέx(ax+b)≤a+b; Δήa<©¹1.Τδ÷–’ΐ¥_ΒΡ «( )
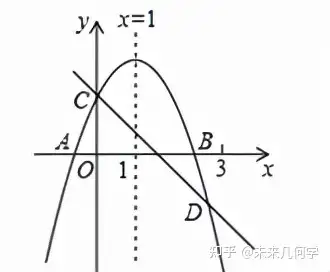
A. ΔΌΔΎΔέΔή B. ΔΌΔΎΔέ C. ΔΎΔέ D. ΔΌΔΎ
ΫβΘΚΓΏ£¹ΈοΨÄ≈cyίSΒΡΫΜϋc(di®Θn)‘ΎxίS…œΖΫ�����Θ§
∴c>0�Θ§
ΓΏ£¹ΈοΨÄΒΡ¨Π(du®§)ΖQίSûι÷±ΨÄx=− b/(2a) =1�����Θ§(άϊ”Ο¨Π(du®§)ΖQίSΙΪ ΫΒΟ≥ωa�ΓΔbΒΡξP(gu®Γn)œΒ)
∴b=−2aΘ§
∴2a+b+c=2a−2a+c=c>0�����Θ§Υυ“‘ΔΌ’ΐ¥_;
ΓΏ£¹ΈοΨÄ≈cxίSΒΡ“Μ²Ä(g®®)ΫΜϋc(di®Θn)‘Ύϋc(di®Θn)(3�����Θ§0)Ήσ²»(c®®)�����Θ§
Εχ£¹ΈοΨÄΒΡ¨Π(du®§)ΖQίSûι÷±ΨÄx=1�Θ§
∴£¹ΈοΨÄ≈cxίSΒΡΝμ“Μ²Ä(g®®)ΫΜϋc(di®Θn)‘Ύϋc(di®Θn)(−1�����Θ§0)”“²»(c®®)�����Θ§
∴°î(d®Γng)x=−1ïr(sh®Σ)�����Θ§y<0����Θ§(¥ζ»κΧΊ β÷Βx=−1�����Θ§ΫY(ji®Π)ΚœàDœώ¨ΔΚ·îΒ(sh®¥)÷Β≈c0Ής±»ί^)
∴a−b+c<0����Θ§Υυ“‘ΔΎ’ΐ¥_;
ΓΏx=1ïr(sh®Σ)Θ§Εΰ¥ΈΚ·îΒ(sh®¥)”–Ήν¥σ÷Β����Θ§(¥ζ»κΧΊ β÷Βx=1�Θ§ΒΟ≥ωΚ·îΒ(sh®¥)Ήν¥σ÷Β����Θ§Εΰ¥ΈΚ·îΒ(sh®¥)ΒΡΥυ”–÷ΒΕΦ–Γ”ΎΉν¥σ÷Β)
∴ax2+bx+c≤a+b+cΘ§
∴ax2+bx≤a+b����Θ§Υυ“‘Δέ’ΐ¥_;
ΓΏ÷±ΨÄy=−x+c≈c£¹ΈοΨÄy=ax2+bx+cΫΜ”ΎC����ΓΔDÉ…ϋc(di®Θn)Θ§Dϋc(di®Θn)‘ΎxίSœ¬ΖΫ«“ôMΉχ‰Υ(bi®Γo)–Γ”Ύ3�����Θ§
∴x=3ïr(sh®Σ)����Θ§“Μ¥ΈΚ·îΒ(sh®¥)÷Β±»Εΰ¥ΈΚ·îΒ(sh®¥)÷Β¥σΘ§
Φ¥9a+3b+c<−3+c�����Θ§(¥ζ»κΧΊ β÷Βx=3Θ§ΫY(ji®Π)ΚœàDœώ¨ΔΕΰ¥ΈΚ·îΒ(sh®¥)÷Β≈c“Μ¥ΈΚ·îΒ(sh®¥)÷ΒΉς±»ί^)
Εχb=−2a����Θ§
∴9a−6a<−3Θ§ΫβΒΟa<−1����Θ§Υυ“‘Δή’ΐ¥_.
Ι ¥πΑΗûιΘΚA.
άΐ2ΓΔ»γàD�Θ§Εΰ¥ΈΚ·îΒ(sh®¥)y=ax2+bx+cΒΡàDœσ≈cyίS’ΐΑκίSœύΫΜΘ§Τδμîϋc(di®Θn)Ήχ‰Υ(bi®Γo)ûι(0.5�Θ§1)Θ§œ¬Ν–ΫY(ji®Π)’™ΘΚΔΌac<0;ΔΎa+b=0;Δέ4ac©¹b2=4a;Δή(a+c)2©¹b2<0.Τδ÷–’ΐ¥_ΒΡ²Ä(g®®)îΒ(sh®¥) «( )
A. 1²Ä(g®®) B. 2²Ä(g®®) C. 3²Ä(g®®) D. 4²Ä(g®®)
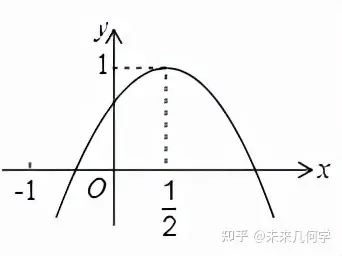
ΫβΘΚ”…àDœώΩ…÷ΣΘΚ
ΔΌa<0, c>0
∴ac<0 ’ΐ¥_
ΔΎΓΏμîϋc(di®Θn)ΒΡôMΉχ‰Υ(bi®Γo)ûι0.5
∴ x=− b/(2a) =1/2
(άϊ”Ο¨Π(du®§)ΖQίSΙΪ ΫΒΟ≥ωa����ΓΔbΒΡξP(gu®Γn)œΒ)
∴a+b=0 ’ΐ¥_
ΔέΓΏμîϋc(di®Θn)ΒΡΩvΉχ‰Υ(bi®Γo)ûι1
∴(4ac - b²)/4a=1(άϊ”ΟΉν÷ΒΙΪ Ϋ)
∴4ac©¹b2=4a’ΐ¥_
ΔΌ °î(d®Γng)x= 1ïr(sh®Σ)Θ§y= a+b+c>0
°î(d®Γng)x= -1ïr(sh®Σ)����Θ§y= a-b+c<0 (a-b+c)(a+b+c)<0
∴(a+c)²©¹b²<0
(¥ζ»κΧΊ β÷Βx=−1Θ§x=1ΒΟΒΫξP(gu®Γn)”Ύa�ΓΔbΓΔc±μΏ_(d®Δ) ΫΏM(j®§n)––œύ≥ΥΫY(ji®Π)ΚœàDœώ¨ΔΚ·îΒ(sh®¥)÷Β≈c0Ής±»ί^)
ΓΓΓΓ ög”≠ Ι”Ο ÷ôC(j®©)�����ΓΔΤΫΑεΒ»“Τ³”(d®Αng)‘O(sh®®)²δ‘LÜ•÷–ΩΦΨW(w®Θng)Θ§2023÷–ΩΦ“Μ¬Ζ≈ψΑιΆ§––����ΘΓ>>ϋc(di®Θn)™τ≤ιΩ¥











